hiltquantum.blogg.se - Solve by substitution

#Solve by substitution how to

We could take this x value to either one of these equations and solve for y. We've done, I guess you can say the hard part, we have solved for x but now we have to solve for y. And we are left with x is equal to 22 divided by 11 is 2, and the negatives cancel out. On the left hand side, we're just left with the -11x and then on the right hand side we are left with -22.

Now to solve for x, we'll subtract 20 from both sides to get rid of the 20 on the left hand side. And now we can combine all the x terms so -3x-8x, that's going to be -11x and then we have -11x+20=-2. We are going to multiply -4*2x which is -8x and -4*-5 is positive 20 and thats going to equal -2. So, it's -3x and then this part right over here we have a -4, be careful, we have a -4 we want to distribute. So now we get just one equation with one unknown. So it's 4(2x-5) and all of that is going to be equal to -2. So this first blue equation would then become -3x-4 but instead of putting a y there the second constraint tells us that y needs to be equal to 2x-5. We can take this constraint, the constraint on y in terms of x and substitute it for y in this first blue equation and then solve for x. They've already made it explicitly solved for y which makes it very easy to substitute for. So, what's neat about this is that they've already solved the second equation. So this is -3x-4y=-2 and then they tell us y=2x-5. 3x-4y=-2 and y=2x-5 So let me get out my little scratch pad and let me rewrite the problem.

And so this is the first exercise or the first problem that they give us. To learn more about how we help parents and students in Markham, Ontario: visit: Tutoring in Markham, Ontario.So that it's less likely that we get shown up by talking birds in the future, we've set a little bit of exercise for solving systems of equations with substitution. We offer tutoring programs for students in K-12, AP classes, and college. SchoolTutoring Academy is the premier educational services company for K-12 and college students. If the x or y of both lines are the same then elimination would be faster. Notice that when x or y has no coefficient, then substitution would be faster. There you go, both methods get you the same answer whenever asked to solve a linear system. Solution: Point of intersection is (-4, 14) Substitute back into Line 1 or 2: y = 6 – 2(-4)ĥ. We either have to subtract or add the variable to get 0y. Line 2: 6x + 2y = 4 (x1) get the lowest common multiple of.

Line 1: 2x + y = 6 (x2) *The ‘y’ variable seems like the simplest to.

This variable can then be substituted back into the other line to find the remaining variable. This removes leaves one variable to solve. Then you would put both lines as if you are adding or subtracting to find a final line just as you would for adding or subtracting large numbers. This method involves “eliminating” one variable by finding the lowest common multiple for a chosen variable. Substitute back into Line 1 or 2: y = 6 – 2(-4)Ĥ. Substitute into Line 2: 6x + 2(6 – 2x) = 4ģ. Once you have the x- and y- coordinates, you then have the solution which is the point of intersection between the two lines.Ģ. This will allow you to isolate and solve for the other variable (y/x).

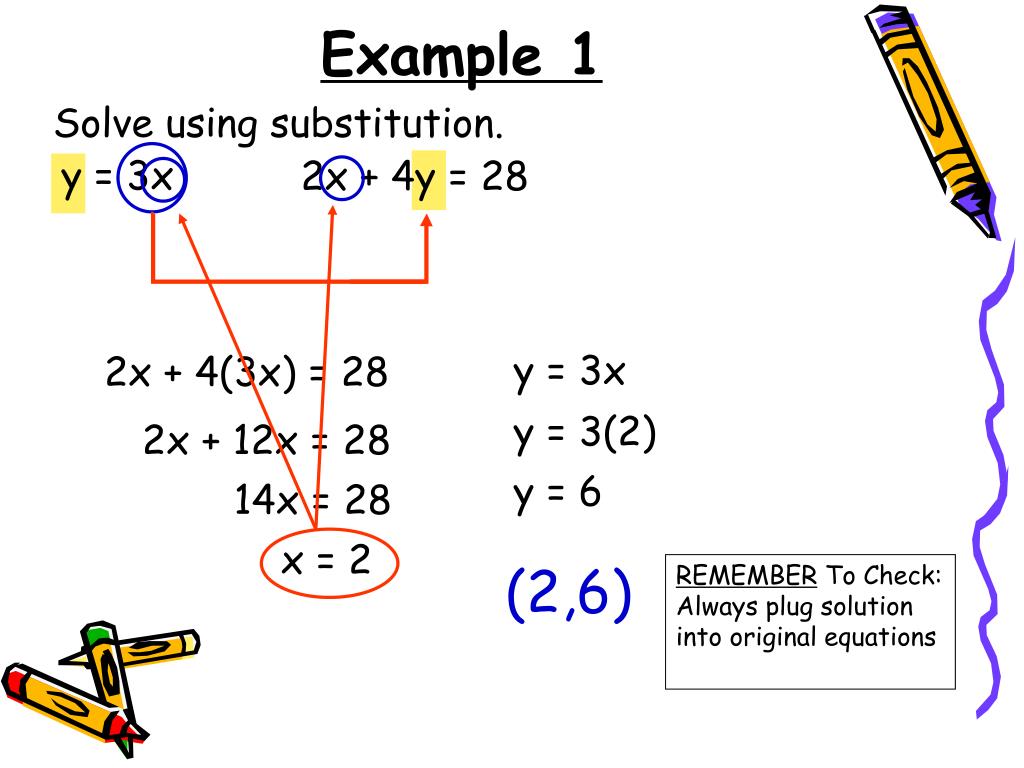
This method involves isolating for one variable (x/y) of Line 1 then substituting that variable into Line 2.

#Solve by substitution how to

The best way to show how to solve these kinds of questions are by providing an example to work on. Both methods will bring you to the same solution but with more practice, you will recognize patterns and see which method would work best when given a system. One is substitution and the other is elimination which is meant to be a shortcut. When dealing with a system of linear equations there are two methods to algebraically solve the question.